Exemplo: programação dinâmica

---

Para entender esse exemplo, você precisa entender a parte de Matemática I, controle de fluxo e funções

---

Nesse exemplo eu vou tratar de resolver um problema de programação dinâmica. Eu vou focar no aspecto de programação e menos em entender o problema: existem excelentes fontes sobre isso e eu escrevi sobre programação dinâmica no Azul. Existem várias variações ao redor do mesmo tema, e o cenário que eu vou adotar é de um agente que tem preferências log e pode acumular capital $k$ e opera uma tecnologia de produção $f(k)=k^\alpha$. O problema do agente é:

$\max \displaystyle \sum_{t=0}^{\infty} \beta^t \log(c_t) \text{sujeito a} k_{t+1} = (1 - \delta)k_t + k_t^\alpha - c_t$

E $\beta$ é a taxa de desconto intertemporal e $\delta$ é a taxa de depreciação. Nosso objetivo é descrever qual a escolha ótima do consumidor, dado a quantidade de capital que ele tem. Para isso, reescreva o problema na forma de Bellman:

$V(k_t) = \max \log(c_t) + \beta V(k_{t+1})$

Onde $V(k_t)$ é a função valor, que não conhecemos. O algoritmo para resolver o problema é bastante simples:

1. Estabela um grid de valores possíveis para $k_t$

2. Dê um chute inicial para os valores da função valor nos pontos do grid

3. Interpole a função valor de alguma maneira

4. Para cada ponto no grid, encontre o valor do consumo que maximiza a equação

5. Salve o valor do máximo em um vetor

6. Itere 3 - 5 até a diferença entre os máximos estarem abaixo de uma certa tolerância

Vamos dissecar as etapas com cuidado.

O grid pode ser igualmente espaçado, então vamos usar o comando range. Como capital deve ser maior que zero, o nosso menor valor vai ser um número pequeno diferente de 0. Vamos colocar 200 pontos.

k_grid = range(1e-7,20,length = 200)

O último valor tem que ser escolhido de maneira que ele não gere problemas no algoritmo: teoricamente nós podemos acumular infinito de capital. Felizmente, retornos decrescentes de escala garantem que se o capital estiver muito acima do valor de steady state, a economia vai despoupar, i.e. reduzir a quantidade de capital.

Nosso chute inicial vai ser bem simples: simplesmente é o valor da função utilidade do nosso agente avaliado no grid. Isso é equivalente a considerar uma escolha de consumir todo o capital no período. Enquanto isso dificilmente é a escolha ótima, é um bom chute inicial (veja Judd (1998)).

u(c) = log(c)
initial_guess = u.(k_grid)

Para interpolar, vamos usar o pacote Interpolations e fazer a interpolação linear entre os pontos.

using Interpolations

inter_value = LinearInterpolation(k_grid,initial_guess, extrapolation_bc = Interpolations.Flat())

Isso vai entrar dentro do loop, então o código acima é apenas um exemplo. Nós temos que fazer de maneira que sempre que atualizamos o nosso chute para a função valor, a interpolação vai ser atualizada também.

O passo 4 involve escrever um loop que passa por todos os pontos do grid, e para cada ponto, encontra o consumo ótimo e o valor da função valor naquele ponto. Um for é perfeitamente adequado para os nossos propósitos. Nós vamos ter que escrever a função a ser otimizada em cada ponto e ela deve receber o consumo, computar o capital remanescente e retornar o valor da função valor naquele ponto, "consultando" a nossa interpolação. A função a ser otimizada, portanto, é:

function V(c)
  k_next = f(k_now) - c + (1-delta)*k_now
  return - u(c) - beta*inter_value(k_next)
end

Veja que como queremos o máximo, eu estou multiplicando a função toda por -1. Além disso, a função recebe parâmetros externos $\beta$ e $\delta$, que não são passados como argumentos da função para facilitar a nossa vida no passo de otimização:

using Optim

for i in 1:length(k_grid)
  k_now = k_grid[i]
  function V(c)
    k_next = f(k_now) - c + (1-delta)*k_now
    return - u(c) - beta*inter_value(k_next)
  end
  resull = optimize(V(c),1e-9,f(k_now) + (1-delta)*k_now)
end

Veja que com isso, somos incapazes de recuperar os valores do resultados. Precisamos colocar os valores da otimização em um array. Nós temos duas estratégias possíveis: podemos criar um array que salva os valores novos e reescreve os valores antigos; ou um array em que cada linha corresponde a uma iteração do algoritmo. Eu vou seguir o segundo método porque ele vai permitir que a gente veja se a diferença entre as funções valores depois de terminarmos. Isso facilita a vida de descobrir se cometemos algum erro no algoritmo. Isso só vai fazer sentido no algoritmo completo, quando consideramos as diferentes iterações.

Eu também vou criar um array que recebe os valores do ponto de ótimo, que são o consumo ótimo para cada valor do estoque de capital. O array se chama policy porque na literatura a escolha ótima em um problema de otimização dinâmica é a "política" - talvez um nome infeliz.

Para a etapa 6, vamos usar um while: enquanto não atingimos o número máximo de iteração OU a diferença entre a função valor for maior que uma tolerância, o algoritmo continua. Isso significa que o while vai receber uma condição E: continue se o número de iteração estiver abaixo do máximo e a tolerância estiver acima da necessária.

No fim, vamos obter algo do tipo:

#Pacotes que vamos usar

using Optim
using Interpolations

#Parâmetros pro algoritmo

iter_max = 400 #número máximo de iterações: depois dissso o programa sai mesmo se não tiver convergência
tol = 1e-9 #Qual a mudança mínima necessária para nós concluirmos que convergiu? Colocamos 1e-9.

u(c) = log(c) #função utilidade
f(k) = k^alfa #função de produção

k_grid = range(1e-7,20,length = 200) #grid de capital

#Parâmetros econômicos, gloriosamente inventados

beta = 0.9 #taxa de desconto
delta = 0.6 #taxa de depreciação
alfa = 0.6 #parâmetro de depreciação

#Arrays que eu vou encher de dados em cada passo do algoritmo

value = zeros(length(k_grid),iter_max) #esse array recebe o valor da função valor
value[:,1] = u.(k_grid) #chute inicial para a função valor
policy = zeros(length(k_grid),iter_max) #esse array recebe os valores de consumo ótimos em cada passo do algoritmo

#Inicializando os parâmetros para o while

error = 1
j = 2

while error > tol && j < iter_max
  inter_value = LinearInterpolation(k_grid,value[:,j-1], extrapolation_bc = Interpolations.Flat()) #interpolação da função valor
  for i in 1:length(k_grid) #iterando nos valores do grid de capital
    k_now = k_grid[i] #só para facilitar a npssa vida: o valor do capital no loop é k_now. Desnecessário, mas deixa o código mais legível.
    function V(c) #definição da função valor - recebe apenas o consumo e calcula todo o resto
      k_next = f(k_now) - c + (1-delta)*k_now #calculando o capital implicado pela escolha de consumo hoje
      return - u(c) - beta*inter_value(k_next) #isso é a equação (2), multiplicada por -1
    end
    resull = optimize(V,1e-9,f(k_now) + (1-delta)*k_now) #otimizando a função valor
    value[i,j] = -resull.minimum #salvando o valor da função valor
    policy[i,j] = resull.minimizer #salvando o consumo no ótimo
  end
  global j = j + 1
  global error = maximum(abs.(value[:,j]-value[:,j-1])) #calculando o erro nessa iteração
end

Onde eu escolhi o valor dos parâmetros que geralmente é usado. Veja que a minha indexação começa em 2 já que a primeira posição do array value é o chute inicial. Veja também que quando salvamos o resultado da otimização nós multiplicamos ele por -1 já que tivemos que multiplicar a função por -1 para encontrar o mínimo.

Ao computar o erro, eu usei o máximo do valor absoluto da diferença entre duas iterações. Isso pode ser visto como uma maneira de dizer que queremos que, mesmo no pior dos casos, a mudança seja abaixo de um certo nível, ou podemos usar uma justificativa matemática um pouco mais formal e dizer que isso é a norma $\ell_{\infty}$.

Vamos fazer uns gráficos para ilustrar. Primeiro, qual a política ótima:

using Plots

plot(k_grid,policy[:,218], legend = :topleft, label = "Consumo")

png("C:\\Users\\User\\Documents\\GitHub\\Julia-Para-Economistas\\Julia Para Economistas\\src\\imagens\\policy_prog_dyn")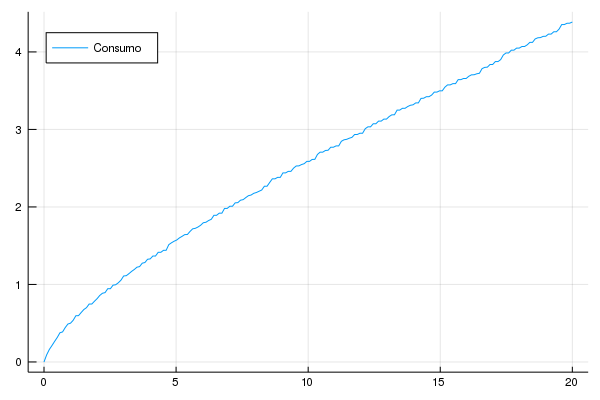

(No meu computador o algoritmo precisou de 219 iterações para convergir. No seu computador, o número pode ser diferente)

Veja que a política ótima implica em um consumo bem abaixo do valor do estoque de capital. Vamos analisar a evolução da função valor para cada iteração:

plot(k_grid[10:200],value[10:200,1], legend = :bottomright, label = "Chute Inicial")
plot!(k_grid[10:200],policy[10:200,20], label = "j = 20")
plot!(k_grid[10:200],policy[10:200,100], label = "j = 100")
plot!(k_grid[10:200],policy[10:200,200], label = "j = 200")

png("C:\\Users\\User\\Documents\\GitHub\\Julia-Para-Economistas\\Julia Para Economistas\\src\\imagens\\value_prog_dyn")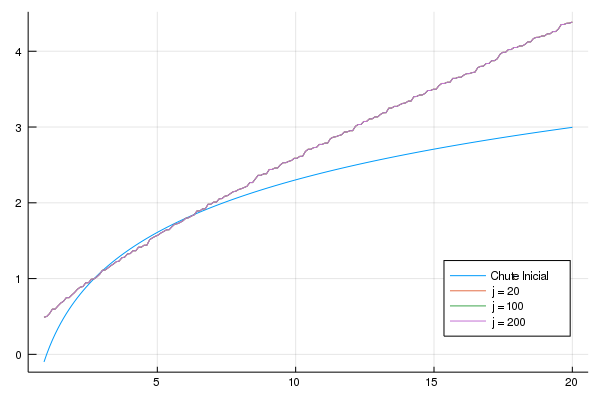

(Eu sou obrigado a cortar os 10 primeiros pontos porque log de um número próximo a zero é um número muito negativo e distorce o gráfico completamente)

Com 20 iterações a função valor já convergiu para a vizinhança do valor final. Isso mostra o quão poderoso é o algoritmo e a matemática por de trás dele