Nessa seção vamos focar nas ferramentas matemáticas que serão úteis para a gente no Julia. Elas em geral vem em forma de pacotes. Nós vamos focar em: otimização, achar a raiz e interpolação. Os pacotes que vamos usar são o Optim, o Roots e o Interpolations. Gráficos também são muito úteis: para saber mais sobre gráficos, visite a parte de gráficos

Optim

Nós já tivemos um primeiro encontro com o Optim em um momento anterior. O Optim faz otimização tanto em funções de uma variável quanto em funções de várias variáveis. Vamos começar com o exemplo que eu já dei:

using Optim

f(x) = x^2

optimize(f,-1,1)

O comando optimize recebe tres argumentos quando buscamos o ótimo de uma função de uma variável: a função, o menor valor do intervalo a ser buscado e o maior valor. Nesse caso, buscamos o mínimo da função f entre -1 e 1. Veja que o comando sempre busca o mínimo: para encontrar o máximo de uma função, basta multiplicar a função por -1. Vamos procurar o máximo da função $\frac{1}{1+x^2}$, que tem a seguinte cara:

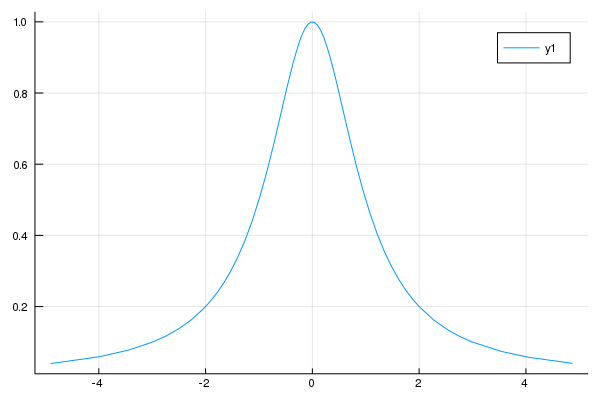
Veja que como queremos o máximo, vamos ter que multiplicar a função por -1. Eu vou definir ela direto com um menos na frente:

l(x) = -1/(1+x^2)
optimize(l,-2,2)

Veja que dessa vez eu deixei o intervalo maior, mas o optimize não deve ter problemas em conseguir achar o mínimo - que no nosso caso é o máximo.

Veja que podemos querer encontrar o ótimo de uma função de várias variáveis. O Optim também nos dá essa possibilidade. Por exemplo, podemos querer achar o mínimo da função $z=x^2+y^2$ - que tem o mínimo em (0,0). Veja que precisamos passar o x e o y como um único elemento em formato de vetor então a função vai ser escrita de maneira um pouco esquisita da segunte forma:

f(x)=x[1]^2+x[2]^2

(Em um pequeno aparte, vale a pena notar que esse mesmo formato de escrever a função para otimizar é utilizado no R)

A função optimize agora recebe a função e um chute inicial, na forma de uma array com o mesmo número de argumentos que a função recebe - nesse caso, 2:

sol = optimize(f,[1,1])

Obviamente um bom chute implica em uma solução melhor. Se dermos um chute em (0,0), o algoritmo não deve fazer nada:

sol = optimize(f,[0,0])

Veja que podemos mudar o algoritmo de otimização. Em geral se usa o Nelder-Mead, que funciona bem para funções não diferenciáveis. Como no nosso caso a função é diferenciável, podemos usar algum outro algoritmo, como o BFGS:

sol = optimize(f,[0,0],BFGS())

Veja que o nome do algoritmo é chamado como se fosse uma função sem argumentos.

O objeto sol contém várias informações: o ponto do mínimo, o valor do mínimo, se houve convergência, em quantas etapas. Em geral, apesar das outras informações serão úteis, nós teremos mais interesse em acessar o ponto do mínimo e o valor no mínimo. Para acessar esses valores usamos uma sintaxe parecida com a do Python: nome do objeto.alguma coisa. No caso, para obter o ponto de mínimo, faríamos sol.minimizer; e o valor no mínimo é obtido pelo sol.minimum.

Roots

O pacote roots permite achar raízes de funções univariadas. Existem quatro maneiras de chamar o comando, mas todos recebem as mesma opções. Vamos tentar achar o zero da função $x+1$ (que convenientemente tem zero em $x=-1$). Vamos usar a função fzero para encontrar o zero dessa função. Ele recebe a função e o limite inferior e o superior para buscar o zero:

g(x) = x-1
zer = fzero(g,-2,0)

A outra opção é usar a função find_zero, que tem sintaxe igual; as funções fzeros e find_zeros, no plural, buscam todos os zeros. Elas são significativamente mais lentos na minha experiência e se você sabe que o problema só tem um zero - pelo menos dentro da região em que ele está buscando - você ganha muita velocidade em usar o fzero ou o find_zero.

Veja que o fato da sintaxe ser parecida com a otimização em uma variável não é mera coinciência: quando otimizamos na mão usando os métodos de cálculo, buscamos o zero da derivada da função $f$. Logo, as semelhanças vão bem além da superfíce do problema.

Interpolations

O pacote Interpolations permite fazer interpolação. A ideia de interpolação é ligar os pontos de alguma maneira. Os Mínimos Quadrados Ordinários (MQO) de econometria são, de certa maneira, um algoritmo de interpolação. Nós também poderíamos querer ligar os pontos de maneira que a nossa função fosse exatamente o valor do ponto - lembre-se que no MQO a reta de regressão em geral não passa exatamente em cima do ponto.

Uma maneira possível de fazer interpolação é, se temos $n$ pontos, podemos construir um polinômio de grau $n-1$ que passe por todos os pontos. Essa não é uma estratégia muito boa: funções simples podem ter aproximações horrorosas por polinômios.

Uma maneira extremamente simples - e fantasticamente útil - de fazer interpolação é "ligar os pontos", como na bricadeira de criança. Podemos ligar os pontos usando retas, o auge da simplicidade: isso se chama interpolação linear. Fazer isso com o Interpolations é bastante simples. O comando LinearInterpolation faz isso para gente.

Como de praxe, é mais fácil explicar com um exemplo: vamos aproximar a função $\frac{1}{1+x^2}$ por interpolação linear. Eu vou gerar 10 pontos equidistantes entre -5 e 5 em um vetor xx e avaliar a função e salvar isso no vetor yy. Depois, eu vou usar o LinearInterpolation para gerar uma função que é a interpolação linear:

f(x) = 1/(1+x^2)

xx = range(-5,5, length = 10)

lin = LinearInterpolation(xx,yy)

Veja que lin é uma função: podemos fazer lin(0.5),por exemplo. Vamos avaliar a qualidade dessa interpolação. Para isso vamos definir uma grade mais fina e avaliar a função e a interpolação:

x = -5:0.01:5
plot(x,f.(x), label = "Função")
plot!(x,lin.(x), line = :dash, label = "Aproximação")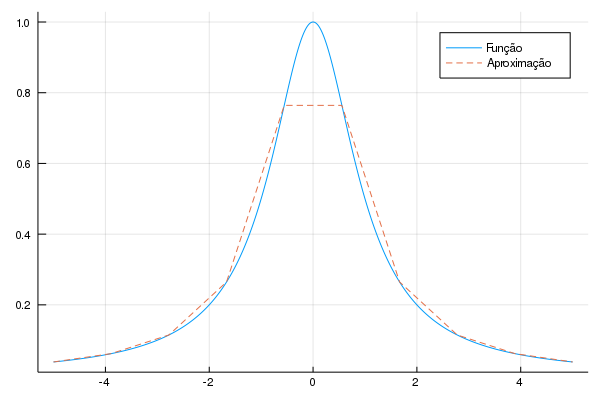

Veja que a aproximação é bastante pouca precisa. Aumentar o número de pontos para 50 melhora bastante a situação:

xx = range(-5,5,length = 50)

yy = f.(xx)

lin = LinearInterpolation(xx,yy)

plot(x,f.(x), label = "Função")
plot!(x,lin.(x), line = :dash, label = "Aproximação")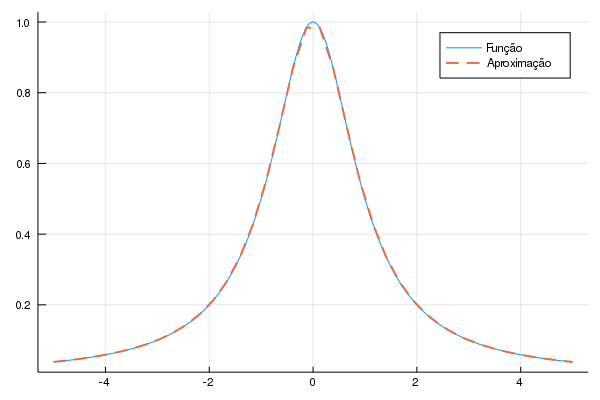

Agora a aproximação é bem melhor - apesar de ser apenas um conjunto de retas.

Às vezes queremos permitir que a função extrapole, i.e., avalie fora da grade que estabelecemos. Para isso, podemos usar a opção extrapolation_bc dentro do LinearInterpolation. Ele aceita várias opções: Flat() repete o último valor; Line() extrapola linearmente, entre outras opções. Eu vou continuar usando a mesma função e focar no que acontece na ponta esquerda quando usamos Flat() e quando usamos Line(). Na ponta direita a figura é idêntica:

x = -7:0.01:-4

lin1 = LinearInterpolation(xx,yy, extrapolation_bc = Flat())
lin2 = LinearInterpolation(xx,yy,extrapolation_bc = Line())

plot(x,f.(x), label = "Função", legend =:topleft)
plot!(x,lin1.(x), line = :dash,w=2, label = "Flat()")
plot!(x,lin2.(x), line = :dash,w=2, label = "Line()")

Nós também podemos querer gerar interpolações de funções que estão definidas não em $\mathbb{R}$, mas em $\mathbb{R}^2$ ou $\mathbb{R}^3$. Nesse caso, o comando passa a ser:

LinearInterpolation((x,y),z)

Onde $(x,y)$ são vetores de tamanho $n_1$ e $n_2$, respectivamente, e z é uma matriz $n_1 \times n_2$.